Hyperbola Calculator

Hyperbola calculator will help you to determine the center, eccentricity, focal parameter, major, and asymptote for given values in the hyperbola equation.

Also, this tool can precisely finds the co vertices and conjugate of a function. In this context, you can understand how to find a hyperbola, it’s a graph and the standard form of hyperbola.

What is Hyperbola?

In mathematics, a hyperbola is one of the conic section types formed by the intersection of a double cone and a plane. In a hyperbola, the plane cuts off the two halves of the double cone but does not pass through the apex of the cone. The other two cones are parabolic and elliptical.

In other words, a hyperbola is a set of all points on the planes, for which the absolute value of the difference between the distances and two fixed points (known as foci of hyperbola) is constant.

How Hyperbola Calculator Works?

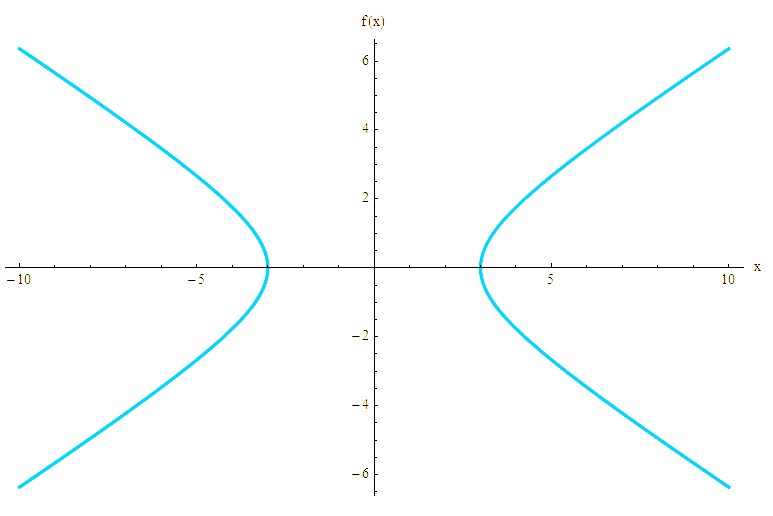
The hyperbola equation calculator will compute the hyperbola center using its equation by following these guidelines:

Input:

• Firstly, the calculator displays an equation of hyperbola on the top.
• Now, substitute the values for different points according to the hyperbola formula.
• Click on the calculate button for further process.

Output:

• The hyperbola calculator provides the equation with input values.
• The calculator displays the results for the center, vertices, eccentricity, parameter, asymptote, directrix, latus rectum, x, and y-intercepts precisely.

FAQ:

What is the parabola in real life?

When the liquid rotates, the gravity forces turn the liquid into a parabolic shape. The most common real-life example is when you stir up lemon juice in a glass or jug by rotating it around its axis.

Is Eiffel Tower a hyperbola?

No, the Eiffel Tower is not an example of hyperbola. It is known to take the form of a parabola.

Is the guitar a hyperbola?

A guitar is a real example of hyperbola because of its different sides and how it’s curved going outwards like a hyperbola. This is an important example for the real world because people who studying to play the guitar and understand it more simply because of its hyperbolic shape.

Reference:

From the source of Wikipedia: As the locus of points, Hyperbola with equation, By the directrix property, Construction of a directrix, Pin and string construction, Steiner generation of a hyperbola.

From the source of Lumen: hyperbola centered at the origin, axes of symmetry, transverse axis, the center of a hyperbola, central rectangle, Equation of a Hyperbola Centered at the Origin.