Parabola Calculator

An online parabola calculator finds the standard and vertex parabolic equations and calculates the focus, direction, vertex, and important points of the parabola. Additionally, the parabola grapher displays the graph for the given equation.

What is Parabola?

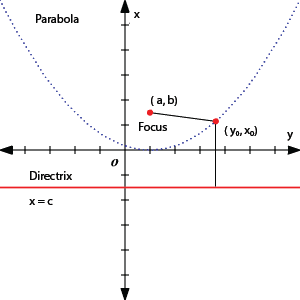
It is defined as a special curve that has shaped like an arch.  It is one of the types of conic sections. This symmetrical plane curve made by the intersection of a right circular cone with a plane surface. This U-shaped curve has some particular properties. In short, it can be concluded that any point on this curve is at equal distance from:

• A fixed point is known as a focus.
• A fixed straight line is known as the parabola directrix.

The standard form to represent this curve is the equation for parabola. Whereas it can be calculated via the parabola equation. All those calculations that involve parabola can be made easy by using a parabola calculator.

Parabola Formula:

• Simplest form of formula is: \(y = x2 \)
• In general form: \( y^2 = 4ax \)

Parabola Equation in Standard Form:

• Parabola equation in the standard form: \( x = ay^2 + by + c\).

However, a parabola equation finder will support calculations where you need to apply the standard form.

Well, the Quadratic Formula Calculator helps to solve a given quadratic equation by using the quadratic equation formula.

Parabola Equation in Vertex Form:

Parabola equation in vertex form: \( x = a(y-k)^2+ h \)

Even the parabola calculator helps to turn the equation into the vertex form through which you can readily find the crucial points of the parabola.

How to Find the Equation of a Parabola?

Well, we can evaluate the axis of symmetry, focus, directrix, vertex, x intercept, y intercept by using the parabola formula in the form of \( x = y^2 + bx + c \).

• Take any parabola equation, and find a, b, c values from equation
• substitute those values in Vertex \( v(h,k) \).
• \( h= \frac {-b}{(2a)}, k = c-\frac{b^2} { (4a)}\).
• focus of the x coordinate is \( \frac {-b}{(2a)} \), and y coordinate is \( c-\frac{b^2-1} { (4a)} \)
• Focus is \( (x,y) \) and Directrix equation \( y = c-\frac{b^2+1} { (4a)}\)
• Axis of symmetry \( \frac {-b}{(2a)} \) and solve y intercept by keeping \(  x = 0 \) in equation.
• Perform these mathematical operations to get required values.

However, an online Discriminant Calculator helps to calculate the discriminant of the quadratic polynomial as well as higher degree polynomials.

Example:

Find axis of symmetry, y-intercept, x-intercept, directrix, focus and vertex for the parabola equation \( x = 11y^2 + 10y + 16 \)?

Given Parabola equation is \( x = 11y^2 + 10y + 16 \).

The standard form of the equation is \( x = ay^2 + by + c \).

So,

$$ a = 11, b = 10, c = 16 $$

The parabola equation in vertex form is \( x = a(y-h)^2 + k \)

$$ h = \frac {-b}{(2a)} = \frac {-10} {(2.11)} = \frac {-10}{ 22}$$

$$h = \frac {-5}{11}$$

$$k = c-\frac{b^2} { (4a)} = 16 - \frac {100} {(4.11)}$$

$$ = \frac {704- 100} {44} = \frac {604} {44} = \frac {151}{44}$$

Vertex is \( (\frac{-5}{11}, \frac{151}{11}) \)

The focus of x coordinate = \( \frac{-b} {2a} = \frac {-5}{11} \)

Focus of y coordinate is = \( c - \frac {(b^2 - 1)} {(4a)} \)

$$= 16 - \frac {(100 - 1)} {(4.11)} =  \frac {16- 99}{44}$$

$$= \frac{704-99} {44} = \frac{605}{44} => \frac {55}{4}$$

Focus is \( (\frac{-5}{11}, \frac{55}{4}) \)

Directrix equation \( y = c - \frac {(b^2 + 1)}{(4a)} \)

$$ = 16 - (100 + 1) / (4.11) =  16- 101/44$$

$$= 704-101/44 = \frac{603}{44} $$

$$ Axis of Symmetry = -b/ 2a = \frac{-5}{11}$$

for y intercept put x is equal to 0 in equation

$$y = 11(0)^2 + 10(0) + 16$$

$$y = 16$$

now x intercept put y is equal to 0 in equation

$$0 = 5x^2 + 4x + 10$$

$$No x-intercept.$$

However, an Online Hyperbola Calculator will help you to determine the center, eccentricity, focal parameter, major, and asymptote for given values in the hyperbola equation.

How to Find the Directrix of a Parabola?

Take a standard form of parabola equation: \( (x - h)2 = 4p (y - k) \)

• In this equation, the focus is: \( (h, k + p)\)
• Whereas the directrix is \( y = k - p \).

If we rotate the parabola, then its vertex is: \( (h,k) \). However, the axis of symmetry is parallel to the x-axis, and its equation will be: \( (y - k)2 = 4p (x - h)\) ,

• Now the focus is: \( (h + p, k)\)
• The directrix of parabola is \( x = h - p \).

Furthermore, the Directrix of a parabola can also be calculated by a simple equation that is: \(y = c - \frac{(b² + 1)}{(4a)}\) .

How Parabola Calculator Works?

Parabola equation calculator makes the calculation faster and error-free as it uses the maths parabola equation. To get convenience, you need to follow these steps:

Input:

• First, select the parabola equation from the drop-down. You can either select standard, vertex form, three points, or vertex and points for input.
• Now, the selected equation for the parabola will be displayed. So just put the values in the given fields accordingly.
• Click the calculate button.

Output:

The Parabola equation calculator computes:

• Parabola equation in the standard form.
• Parabola equation in the vertex form.
• All the parameters such as Vertex, Focus, Eccentricity, Directrix, Latus rectum, Axis of symmetry, x-intercept, y-intercept.
• Provide step-by-step calculations, when the parabola passes through different points.
• Along with all these mathematical values, this parabola grapher displays the graph of the parabola in the end.

FAQs:

How does the distance between the focus and the Directrix affect the shape of a parabola?

Whenever the distance between the focus and parabola directrix increases, |a| will decrease. It means that the parabola gets widen with the increase of distance among its two parameters.

What are the steps to graphing a parabola?

For quick and easy calculations, you can use an online parabola grapher that plots the graphical representation of the given parabola equation. However, for manual plotting of parabola graph you have to follow some steps:

• First of all, find the following parameters:
• y-intercept.
• x-intercepts.
• Look for some extra points to have at least five points to plot graph.
• Now just Plot the points and sketch your parabola graph.

What are the two types of transformation?

The first type of transformation is known as Translation. It shifts a node from one position to the other along with one of the axes that are related to its initial position.

The second type is Rotation. It moves the node in a circle around a pivot point.

How do you describe the transformation of a parabola?

Translating a parabola vertically gives you an opportunity to produce a new parabola. It will be the same as the basic parabola. In the same way, you can translate the parabola horizontally.

Conclusion:

Parabola calculator used to get quick results and obtain the graph for any given parabolic equation. This parabola equation finder makes your calculation faster and easy by solving all the related properties of the parabolic equation. It lets you understand how to put the values in the parabola formula as well. So, this tool always ready to provide its services to everyone in the blink of an eye and without any cost.

References:

From the source of Wikipedia: Cartesian coordinate system, Similarity to the unit parabola, Position of the focus.

From the source of Paul's online Notes: Parabolas, Sketching Parabolas, Axis direction.

From the source of OER Services: Graphing Parabolas with Vertices at the Origin, Standard forms of parabolas with vertex, The x-axis as the axis of symmetry.

Other Languages: Parabol Hesaplama, Kalkulator Parabola, Kalkulator Paraboli, Parabel Rechner, 放物線 計算.