Absolute Value Calculator

Absolute value calculator provides the absolute values of real values and functions separately for the given values. Our calculator provides all the important information about inequalities and absolute functions.

What are the Absolute Values?

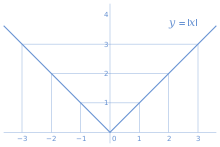
In mathematics, the absolute value or modulus | x | of the real number x is the non-negative value of x, regardless of its sign. That is | x | = x means positive x, | x | = -x means negative x (in this case -x is positive), and | 0 | =0.

Graph for Absolute Values:

The general form of absolute value notation equation is:

F(x) = k + a |x – h|

This equation used by the absolute value graph calculator, where, k and h tell about how the graph shifts vertically and horizontally. The variable “a” tells us how far the value graph stretches vertically, and whether the graph opens down or up.

How to Solve Absolute Value Equations?

Solving absolute value equations is simple as using ordinary linear equations. The only additional important step is to divide the original absolute value equation into two parts: positive and negative (±) components.

• Symbol ∣x∣ must be positive. For example, |x∣→+ ∣x∣.
• x in the absolute value symbol | | can be any equation.
• To be solved, the right side of the equation must be a positive number or zero.
• If the “a” on the right is negative, then it has no results.

Example:

Solve the absolute value equation − ∣ x ∣ = −9.

Solution:

Don’t come to the conclusion that this equation has no solution too quickly. Although the right side of the equation is a negative number, the absolute value expression itself must be a positive number. this is not RIGHT?

• The | x | sign must be positive. Emphasize | x ∣ → + ∣ x∣.
• An absolute value calculator removes the minus sign from the absolute value sign before we can continue.
• The coefficient of this equation is -1. So, the absolute value function calculator divides both sides of the equation by this value to remove the negative sign.

-|x| = -9

-1 . |x| = -9

-1 . |x| / -1 = -9/-1

|x| = 9

• Since the absolute value expression and the number are positive, the absolute value equations calculator uses a process to divide them into two equations.

|x| = a => x = +a, x = -a

• So, the solution of the problem becomes

|x| = 9 => x = 9, x = -9

How Absolute Value Calculator Works?

Our absolute value equation calculator changes the input values into the positive number and check the particular points of the absolute value graph and equation with the following steps:

Input:

• Click the “number tab”, if you want to perform a mathematical operation on a given number, or select “for equation” tab, when you want to solve an equation.
• Now, substitute the given values in the selected tab fields.
• Click on the calculate button for the solution.

Output:

• The absolute value inequalities calculator solves the number or equation for absolute values according to your selection.

Reference: 

From the source of Wikipedia: Terminology and notation, Definition and properties, Complex numbers, Proof of the complex triangle inequality, Absolute value function.