Linear Interpolation Calculator

An online linear interpolation calculator helps to find the interpolated values for the data points on a line or a curve. The calculator plots the interpolated point on a line and shows a step-by-step solution by using linear interpolation formula.

Just read the context to get the basic insight about how to do interpolation, its formula, and some standard terms that help to understand interpolating.

What is Linear Interpolation in Math?

Linear interpolation is a method of creating new data points in an already known discrete set of data points. In this mathematical procedure, some original data points can be interpolated to produce a simple and new function that will be close to the original data. This integration of new value is known as interpolating. In other words, we can also say that a Linear interpolant is a straight line that exists between the two recognized co-ordinate points (x0, y0) and (x1, y1). You can readily find the interpolant value between the two coordinates on a straight line by using a linear interpolation calculator.

Linear Interpolation Formula:

Formula for Linear interpolation is

$$y = y1 + ((x – x1) / (x2 – x1)) * (y2 – y1)$$

In this interpolation equation:

• X = known value,
• y = unknown value,
• x1 and y1= coordinates that are below the known x value
• x2 and y2 = coordinates that are above the x value.

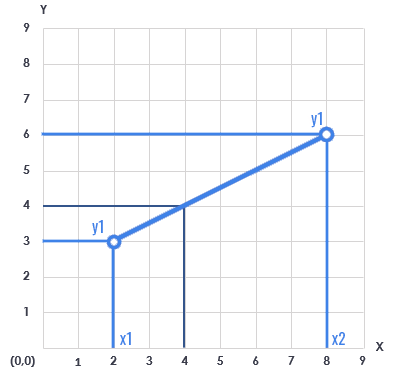
Moreover, an Online Slope Calculator helps to find the slope or gradient points A (x1,y1) and B (y1,y2) in the Cartesian coordinate plane.

Example1:

If the Given data points are (2, 4) and (6, 8), how will you calculate the value of y when x = 2.

In the first step, we will Extract the coordinates of the given data points.

$$x1=2$$

$$y1=4$$

$$x2=6$$

$$y2=8$$

In the second step, we will take the following equations to have the values of m and then y

• \(m = y2 − y1 / x2−x1\) = equation 1
• \(y = y1+m * (x–x1) \)= equation 2
• To calculate the value of m put the values in equation 1, \(= m=8−4 / 6−2 = 1\)
• Now we have a value of m therefore we will use equation 2 to find out the value of y.
• \(y=4+1 * (2–2) = 4\)

Meanwhile, x is within the interval \([x1, x2]\), so we have done a linear interpolation calculation to find the value of y.

However, An Online Centroid Calculator helps you to find the centroid of a triangle (ABC), N-Points, and N-sided polygon for the given coordinates.

Example 2:

Find the value of \(y^2\) on a given line while the given data is

“$$x1 = 4, y1 = 6, x2 = 8, x3 = 12, y3 = 14$$”.

Solution:

As We have linear interpolation equation:

$$y_2= (x_2 – x_1) x (y_3- y_1) / (x_3 – x_1) + y_1$$

A step by step solution to find y2 will be as by putting the in above equation as follows:

$$y_2= (x_3−x_2) x (y_3−y_1) / (x_3−x_2) +y_3$$

$$y_2= (12−8) x (14−6) / (12−8) +14$$

$$y_2= (4) x (8) / (4) +14$$

$$y_2= (32) / (4) +14$$

$$y_2=8+14$$

$$y_2=22$$

How Linear Interpolation Calculator Works?

Here is the working procedure of the online calculator to figure out the linear interpolated values.

Input:

• Enter the 5 different data points to find the linear interpolated value of a specific point and to perform the interpolation.
• Click the calculate button

Output:

The online interpolation calculator will provide you the following results:

• A new interpolated value will be displayed at that point where we want to conduct interpolating.
• This interpolator will plot a point of interpolation on a line.
• The input data points and linear interpolation formula
• It will give you a detailed step-by-step solution for the calculated interpolated value.

Frequently Asked Questions (FAQs):

Which method can be used in any question of Interpolation?

Usually, we use the Polynomials interpolating method. The reasons to use polynomials are:

• It is easy to evaluate them
• Differentiation and integration are easy.

This is known as polynomial interpolation.

When should Interpolation be used?

As we already know that with Interpolation we can find out unknown points therefore It can be used whenever we need to predict unknown values for any geographic point data. It is helpful for the prediction of rainfall, resulted in chemical concentrations, assess the noise levels, and so on.

Which is the best Interpolation method?

Inverse Distance Weighted (IDW) interpolation is considered as one of the best methods to achieve better results than any other interpolation method.

Is kriging an Exact Interpolation?

kriging interpolation technique is generally linked with exact interpolation. All the Kriging predictions can change progressively in space. They will case to change after getting to a location where data has been composed. At this point, there is a “jump” in the prediction to the most precise value that was first measured. However, an interpolator can be used to make quick and accurate predictions.

Final Point:

Thanks to the linear interpolation calculator for finding the unknown data point for given coordinates and plot the point on graphs. Also, this tool shows the formula which is used to fulfill the requirements with complete calculations step by step to facilitate the end-users with-in no time. It provides its support for learning and educational purposes without any cost. Hence let’s try to find the answer by putting the known data point in this interpolator!

Reference:

From the source of Wikipedia: Linear interpolation between two known points, Interpolation of a data set, Linear interpolation as an approximation.

From the source of Science Direct: Linear Interpolation, The coupling methods,

The interpolating polynomial.

From the source of Dagra: Linear Interpolation Equations, Linear interpolation methods.

Other Languages: Kalkulator Interpolasi, Interpolacja Kalkulator, Interpolation Rechner, Interpolasyon Hesaplama, 補間計算, Calculadora De Interpolação, Calcul Interpolation Linéaire, Interpolar Calculadora, Calcolo Interpolazione Lineare, Калькулятор Интерполяции, Lineární Interpolace Výpočet, حاسبة الاستيفاء, Interpolointi Laskin.