Local Maxima and Minima Calculator

An online local maxima and minima calculator has been specially designed for scholars and mathematicians to get instant outputs regarding maxima and minima.

Below in this read, we will be discussing what are local maxima, local minima, and how to figure out these parameters either manually and using free local minimum and maximum calculator.

Let’s indulge together!

What Are Local Maxima And Minima?

In the contextual of mathematical analysis, we have:

Local Maxima:

The point (x, y) on a function f(x) whose y coordinate is greater than all the y coordinates of other points that are actually close to (x, y).

Local Minima:

A particular point (x, y) on the function’s graph whose y coordinate is the smallest for all other y coordinates of other points that are close to (x, y).

Determination of Local Maxima And Minima:

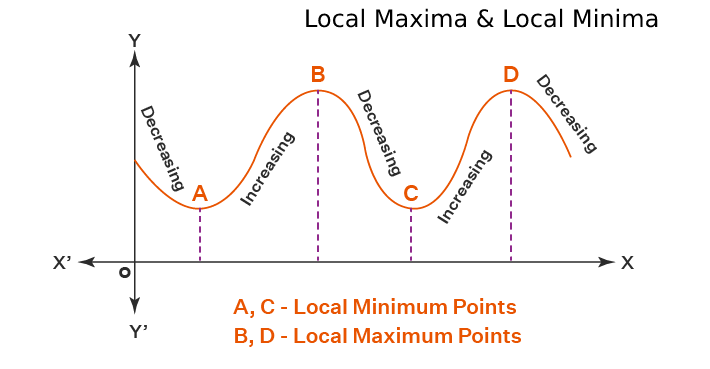
The most reliable method of finding local maxima and minima of any function is the local maxima and minima calculator. But you must be able to comprehend the manual calculations. Following are the key points that you must keep in mind when finding local maxima and minima of the function:

Take Derivative of the Function:

When you have a function, you first look whether this function is differentiable or not. If it is, then determine the derivative of the function. Moreover, you can also use our best derivative calculator to find the derivative of any function within a span of seconds. It will definitely help you out in minimising your calculations time and improve accuracy.

Factorize the Resulting Derivative Function:

After you differentiate the function into smaller values, go for finding the factors of the function. One thing here is that factoring may demand some extra time to think of the numbers that may satisfy the given function. That is why you can use our factoring calculator to determine the factors of any function immediately. How does it sound?

Determine Critical Points:

So the next method is the determination of the critical points, the points where the function is not able to differentiate. You can find these points by putting the factors equal to zero and solve for a particular value of x. But in case you find it difficult, our critical point calculator will be doing that for you in seconds.

Find Local Maxima & Minima:

At the end, put critical point values in the original equation one by one to determine the local maxima and minima of the function. But by commencing to our best online local maxima and minima calculator, you could definitely determine all of the above parameters with a couple of clicks.

How To Find Local Maxima And Minima?

Okay let us move towards resolving an example that will clarify your concept about the parameters under discussion.

Example # 01:
How to find local max and min of the following differentiable function:
$$ 4x^{3} + 3x^{2} $$

Solution:
Here we have:

$$ 4x^{3} + 3x^{2} $$

Finding derivative:
$$ 4x^{3} + 3x^{2} $$
$$ \frac{d}{dx}{4x^{3} + 3x^{2}} $$
$$ 12x^{2} + 6x $$

Determining factors:
$$ 12x^{2} + 6x $$
$$ 6x\left(2x + 1\right) $$
$$ Factors = 6x \hspace{0.025in} and \hspace{0.025in} 2x+1 $$

The free online local maxima and minima calculator also find these answers but in seconds by saving you a lot of time.

Critical points:
Putting factors equal to zero:

$$ 6x = 0 $$
$$ x = 0 $$
And

$$ 2x+1 =0 $$
$$ x = -\frac{1}{2} $$

Local Maxima & Local Minima:
Here we have:
$$ 4x^{3} + 3x^{2} $$
Putting \(x=0\) in above equation:
$$ 4x^{3} + 3x^{2} $$
$$ = 4\left(0\right)^{3} + 3\left(0\right)^{2} $$
$$ = 0 $$
As we got zero, this value represents the local minima.

So we have:
$$ 4x^{3} + 3x^{2} $$
$$ 4\left(-\frac{1}{2}\right)^{3} + 3x^{2} $$
$$ \frac{-4}{8} + \frac{3}{4} $$
$$ \frac{-4+6}{8} $$
$$ \frac{2}{8} $$
$$ \frac{1}{4} $$

Result:
Local maxima: (-½, ¼)
Local minima: (0, 0)

How Local Maxima And Minima Calculator Works?

Let this free minimum maximum calculator find the smallest and largest values of any function within a couple of seconds. Want to know how it actually works? Let us go!

Input:

• What you need to do is just write your function equation in the designated field
• After that tap the calculate button

Output:
The free local min and max calculator determines:

• Derivative of the function
• Factors of the derivative function
• Critical points of the function
• Local maxima and minima

FAQ’s:

What is the difference between local maxima and absolute maxima?

Absolute maxima is the value of the function that is greatest and remains throughout the whole domain of the function. On the other hand, local maxima is the maximum value of the function but it lies in the subset of the domain. One interesting fact is that you can go for finding all these parameters immediately by subjecting yourself to a free local maximum and minimum calculator.

What is absolute minima?

The absolute minima are the points that go for representing the smallest value of the function which remains constant throughout the whole domain. You can also determine the absolute minima with the assistance of a free online local max and min calculator easily.

What is the point of inversion?

Any value of x within the function’s domain that is neither maximum nor minimum is known as the point of inversion. Keep in mind that the most immediate points on the left or right side of the inversion point have a slope of zero.

What is the extreme value theorem?

If a function is defined and continuous within the interval [a, b], there are points c and d that are present within the interval [a, b]. For these values, the function f gets maximum and minimum values.

f(c) > f(x) > f(d)

What is the local minimum of the function as below:
f(x) = 2

As the derivative of the function is 0, the local minimum is 2 which can also be validated by the relative minimum calculator and is shown by the following graph:

Can we consider all global maxima as the local maxima?

Global maxima are always one value, respectively. But when we talk about the local maxima, there is more than one. The other reason is that global maxima is the largest value while local maxima is the largest value in the subset domain. That is why, global maxima can not be considered the local maxima.

What is the local minima in an array?

If the number in an array is smallest from both left and right side numbers of it, then it is called the local minima in an array.

For example:

Look at the following number array:

4, 4, 6, 3, 3, 2, 4, 5, 7

In the above array, the number 2 is considered as the local minima of the array as both the number on the left and right side of it are greater than it and are 3 and 4, respectively.

Note: the process gets vice versa in case you are interested in determining the local maxima of the array.

Conclusion:

Well, so far we had a brief outlook of the conceptual theory of maximum and minimum values of the function. The basic fact behind this contextual and design of this free local maxima and minima calculator is that this is widely used to estimate various phenomena. The most crucial of which include estimation of the rocket height that it will attain after its launch, the maximum or minimum amount of the aluminium that will be required to make the number of tin cans, and resolving many other optimization problems.

References:

From the source of wikipedia: Maxima and minima, Functions of more than one variable, In relation to sets

From the source of khan academy: Absolute maxima and minima, Relative maxima and minima

From the source of lumen learning: Maxima and Minima, Absolute Extrema, Local Extrema And Critical Points, Locating Absolute Extrema