Beam Deflection Calculator

Beam Deflection Calculator

Select the beam type, load type, and enter the necessary values. The tool will instantly calculate the beam deflection for you.

Beam Type:

Load Type:

Span Length, L:

m ▾

Uniform load, w:

N/m ▾

Uniform load, w:

N.m ▾

Point Load, P:

kN ▾

Modulus of Elasticity, E:

kPa ▾

Moment of Inertia, Ix:

m⁴ ▾

Distance:

m ▾

Deflection At:

Make use of our beam deflection calculator to find maximum deflection of the beam (simple-supported or cantilever) after a certain load is carried on it. Calculates the effect of beam bending depending upon the magnitude and location of the object placed on it.

How To Calculate Beam Deflection?

Following beam deflection formulas will help you out in determining the respective beam deflections for certain loads it carries:

Simply-Supported Beam:

Midspan Load:

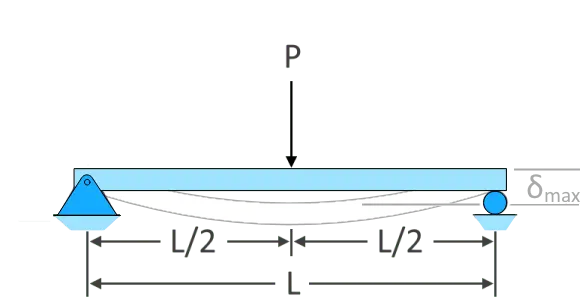
Midspan Beam

\(𝛿_{max}=\dfrac{PL^{3}}{48EI}\)

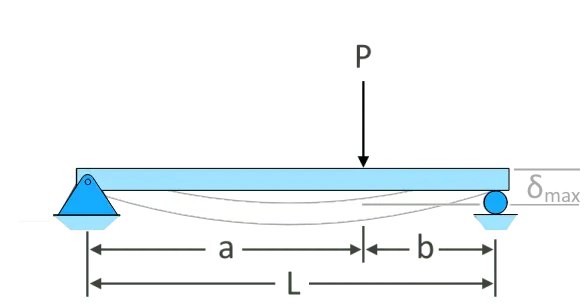
Load at Any Point:

Load at any point

\(𝛿_{max}=\dfrac{Pb\left(3L^{2}-4b^{2}\right)}{48EI}\)

Uniform Load:

Load at any point

\(𝛿_{max}=\dfrac{5wL^{4}}{384EI}\)

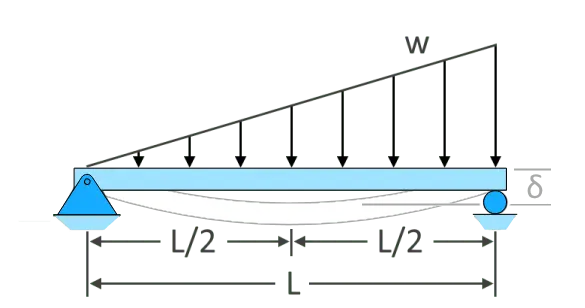
Uniformly Varying Load:

Uniformly varying load

\(𝛿_{max}=\dfrac{0.00652wL^{4}}{EI}\)

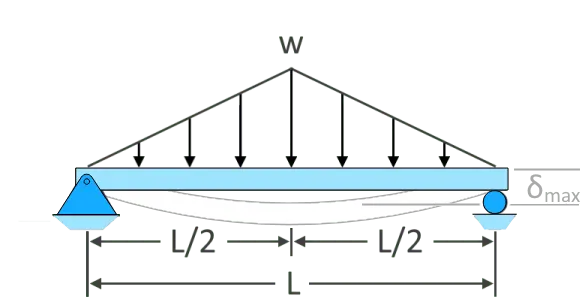
Triangular Load:

Triangular load

\(𝛿_{max}=\dfrac{wL^{4}}{120EI}\)

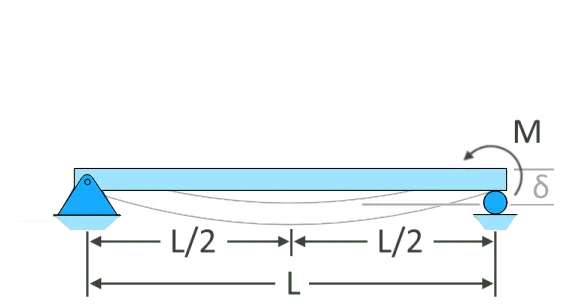
Moment Load at Some Support:

Moment load at some support

\(𝛿_{max}=\dfrac{ML^{2}}{9\sqrt{3}EI}\)

Cantilever Beam:

For these specific types of beam, our steel i beam deflection calculator different equations that are as follows:

End Load:

End load

\(𝛿_{max}=\dfrac{PL^{3}}{3EI}\)

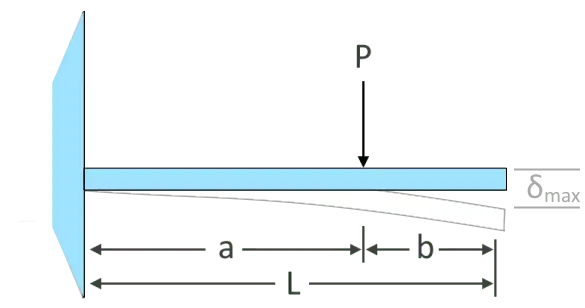
Load at Any Point:

Load at any point

\(𝛿_{max}=\dfrac{Pa^{2}\left(3L-a\right)}{6EI}\)

Uniform Load:

Uniformly Varying Load (Case 1):

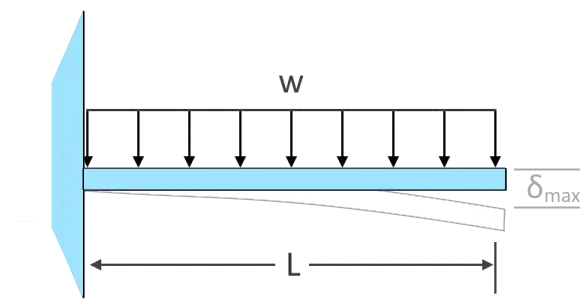
Uniform Varying load

\(𝛿_{max}=\dfrac{wL^{4}}{30EI}\)

Uniformly Varying Load (Case 2):

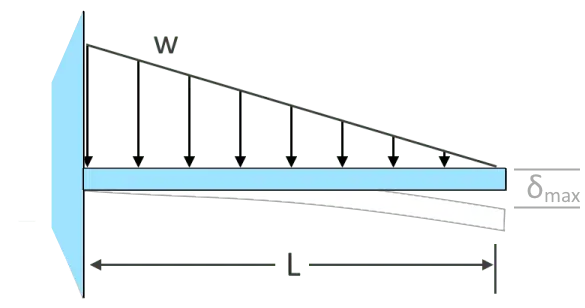
Uniform varying load at beam

\(𝛿_{max}=\dfrac{11wL^{4}}{120EI}\)

Moment Load at End:

Moment load at end

\(𝛿_{max}=\dfrac{ML^{2}}{2EI}\)

How to Use This Beam Deflection Calculator?

To use this beam deflection calculator, follow the below-mentioned steps:

Select the “Beam Type” and “Load Type.”
Enter the length of the span and the point load.
Input the modulus of elasticity and moment of inertia.
Hit the “calculate” button.

References:

From the source of Wikipedia: Deflection (engineering), Beam deflection for various loads and supports, Units From the source of Lumen Learning: Stress, Strain, and Elastic Modulus, Tensile or Compressive Stress, Bulk Stress