SAS Triangle Calculator

Give a try to our free SAS triangle calculator to find each and every entity of a triangle. Just provide a couple of adjacent sides of the triangle and their mutual angle and let the calculator do the rest for you.

What Is A SAS Triangle?

In Trigonometry, SAS corresponds to a Side-Angle-Side triangle.

How to Solve SAS Triangle?

What if you think about how to find the angle of a triangle given 2 sides and 1 angle. Let us tell you!

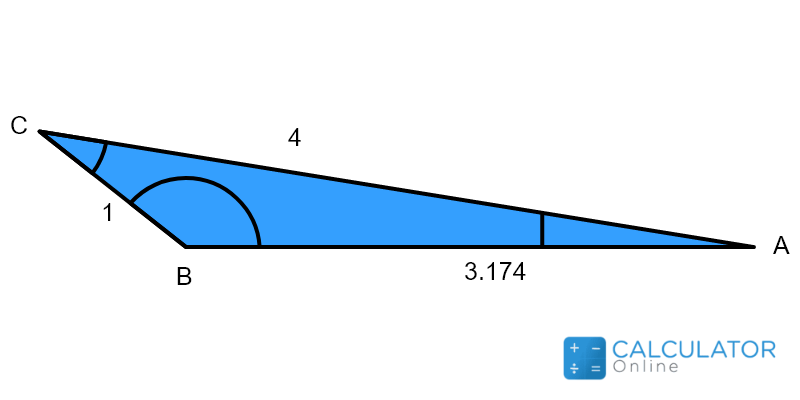
Suppose we have to solve triangle SAS given as under:

In this triangle, we are given:

\(a = 1\)

\(b = 4\)

\(γ = 30^{\text{o}}\)

Third Side c:

By using law of cosines:

\(c=\sqrt{\left(1\right)^{2}+\left(4\right)^{2}−2 \text{1*4 } cos\left(30^{\text{o}}\right)}\)

\(c=3.17\) For calculations, tap law of cosine calculator.

For other sides, you may use:

\(a=\sqrt{b^2+c^2−2 \text{ b c } cos(α)}\)

\(b=\sqrt{a^2+c^2−2 \text{ a c } cos(ꞵ)}\)

Perimeter:

\(p=a+b+c\)

\(p=1+4+3.17\)

\(p=8.17\)

Semiperimeter:

\(s=\dfrac{p}{2}\)

\(s=\dfrac{8.17}{2}\)

\(s=4.085\)

Area:

By using the Heron’s formula:

\(A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}\)

\(A=\sqrt{4.085\left(4.085-1\right)\left(4.085-4\right)\left(4.085-3.17\right)}\)

\(A=\sqrt{1}\)

\(A=1\)

Height of Triangle:

\(h_{a}=\dfrac{2A}{a}\)

\(h_{a}=\dfrac{2*1}{1}\)

\(h_{a}=2\)

\(h_{b}=\dfrac{2A}{b}\)

\(h_{b}=\dfrac{2*1}{4}\)

\(h_{b}=\dfrac{1}{2}\)

\(h_{b}=0.5\)

\(h_{c}=\dfrac{2A}{c}\)

\(h_{c}=\dfrac{2*1}{3.17}\)

\(h_{c}=0.630\)

Inner Angles:

By using law of sines here:

\(\dfrac{b}{sinꞵ}=\dfrac{c}{sin𝛾}\)

Rearranging for missing angle:

\(sinꞵ=\dfrac{b}{c}*sin𝛾\)

\(sinꞵ=\dfrac{4}{3.17}*sin\left(30^{\text{o}}\right)\)

\(sinꞵ=1.261*0.5\)

\(sinꞵ=0.6305\)

\(ꞵ=sin^{-1}\left(0.6305\right)\)

\(ꞵ=140°\)

Now using the supplementary angle measurement

\(𝛼+𝛽+𝛾=180^{\text{o}}\)

\(𝛼+140°56′7″+30°=180^{\text{o}}\)

\(𝛼=180^{\text{o}}-140°-30°\)

\(𝛼=10^{\text{o}}\)

Inradius:

\(r=\dfrac{A}{s}\)

\(r=\dfrac{1}{4.085}\)

\(r=0.244\)

Circumradius:

\(R=\dfrac{a*b*c}{4r*s}\)

\(R=\dfrac{1*4*3.17}{4*0.244*4.085}\)

\(R=3.17\)

Medians:

\(m_{a}=\sqrt{\dfrac{2b^2+2c^2-a^2}{2}}\)

\(m_{a}=\sqrt{\dfrac{2*4^2+23.17^2-1^2}{2}}\)

\(m_{a}=3.576\)

\(m_{b}=\sqrt{\dfrac{2c^2+2a^2-b^2}{2}}\)

\(m_{b}=\sqrt{\dfrac{23.17^2+21^2-4^2}{2}}\)

\(m_{b}=1.239\)

\(m_{c}=\sqrt{\dfrac{2a^2+2b^2-c^2}{2}}\)

\(m_{c}=\sqrt{\dfrac{21^2+24^2-3.17^2}{2}}\)

\(m_{c}=2.446\)

How Does SAS Triangle Calculator Work?

If you wish to use our SAS calculator, read on and understand the following guide!

Input:

• Enter two side and their associated angle measure
• Hit the calculate button

Output:

• The side angle side calculator complete the solution of SAS triangle

References:

From the source of Wikipedia: Triangle, Types of triangle, Basic facts, Existence of a triangle, Points, lines, and circles associated with a triangle, Computing the sides and angles

From the source of Tutors.com: Triangle Congruence Postulates: SAS, ASA, SSS, AAS, HL

From the source of Lumen Learning: A Bit of Geometry, Similar Triangles