Difference Quotient Calculator

An online difference quotient calculator allows you to determine the difference quotient for a given function. This simplifying differential quotient calculator displays stepwise calculations to measure the slope of the secant line which passes through two points. In this context, you can learn how to find the difference quotient using its formula. Let’s start with some basics!

What is the Difference Quotient?

In calculus, difference Quotient is used to measure the slope of the secant/curved line between the two different points on the graph of a function. A function is a curve or line that has one “y” value for every “x” value. Therefore, the slope defines the derivation of a function.

In simple words, the difference quotient measures the rate of change of a function f(x) with respect to x in a given interval [x, x + h].

(Image)

However, the Online Secant Calculator helps you to find the secant of the given angle in degree, radian, or the π radians.

Difference Quotient Formula:

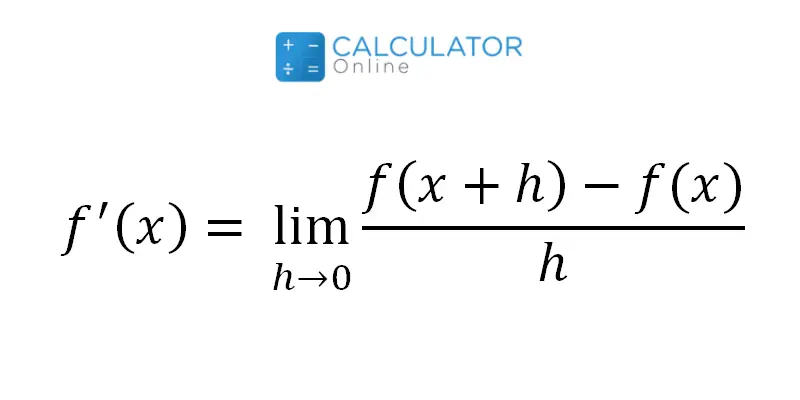
The difference quotient equation measures the approximated form of derivative as:

$$ f(x) = f(x + h) – f(x) / h $$

Where “h” is the step size and f(m) is a function. This computes the rate of change of given function f(x) over the interval [x, x + h].

How to Find Difference Quotients?

Here are some steps to remember when measuring difference quotients:

• Evaluate the expression of f (m + h) by substituting m in f (m) with m + h.
• Now, evaluate the expression of f (n) by plugging in f (m) with n.
• Then, evaluate the difference between the two points and divide the given expression by h.

Well, you don’t need to remember formulas and steps, if you use this simplify the difference quotient calculator. Simply, substitute the given function and it’ll provide a stepwise solution quickly.

Difference Quotient Example:

Example #1:

Solve difference quotient of a function (f) defined by

$$ F(x) = x^2 + 4 $$

Solution:

Formula to find Difference Quotient is:

$$ f(x) = f (x + h) – f (x) / h $$

To find f(x + h), put x + h instead of x:

$$ f (x + h) = (x + h)^2 + 4 $$

Then,

$$ f(x) = f (x + h) – f (x) / h $$

$$ f(x) = ((x + h)^2 + 4) – (x^2 + 4) $$

$$ = h + 2x $$

Thus, the difference quotient for f (x) = x^2 + 4 is h + 2x. You can find it by substituting these values into the simplified difference quotient calculator.

Example #2:

Find and simplify the difference quotient of the function f(x) = 4x – 5.
Solution:
Using the difference quotient formula,
Difference quotient of f(x)
= [ f(x + h) – f(x) ] / h
= [ (4(x + h) – 5) – (4x – 5) ] / h
= [ 4x + 4h – 5 – 4x + 5 ] / h
= [ 4h ] / h
= 4
Hence, the difference quotient of f(x) is 4.
You can verify the above results with the help of our free online find the difference quotient calculator.

However, an online Derivative Calculator will allow to calculate the derivative of the function with respect to a given variable.

Symmetric Difference Quotients:

In mathematics, the difference quotient formula gives the approximations of the derivation of a function. There are many difference quotients such as symmetric and one-sided difference quotient. These are related to each other and gives a good approximation than others due to this relation.

The symmetric derivative is generalizing the ordinary derivative which can be defined as:

Lim_{h →0} \frac {f (a + h) – f (a – h)} {2h}

A function is symmetrically differentiable at the point “a” if its derivative exists at that particular point. An expression under the limit is called a symmetric difference quotient.

Apart from that, f(x+h)-f(x)/h is a formula that is a function of the limit definition of the derivative (first principles).
The limit definition of the derivative of a function f(x) is defined as:
f'(x) = lim ₕ → ₀ [ f(x + h) – f(x) ] / h.

Also, try our online f(x+h)-f(x)/h calculator to determine the limit definition of the function’s derivative.

How Does the Difference Quotient Calculator Step by Step Work?

An online difference of quotient calculator computes the slope of the curved line between two different points by following these instructions:

Input:

• Enter a function (f) with respect to any variable from the drop-down list.
• Hit the calculate button to continue the process.

Output:

• The limit of difference quotient calculator displays difference quotients for the given function.
• The simplifying the difference quotient calculator provides the formula to calculate the difference quotients with stepwise calculations.

FAQ:

Who found the difference quotient?

The difference quotient is also known as the Newton quotient. Isaac Newton (1671) used zero (0) in his process of fluxions, which is an infinitely small increment of the independent variable.

Does the average rate of change the same as slope?

The average rate of change is the transformation in values of the y variables to the change in values of the variables of x. If the rate of change is linear and constant, then it is the slope of the line. The slope of a curved line may be negative, positive, zero, or undefined.

What is a quotient function?

The quotient function returns the integer part of a division. There are two arguments, the denominator is the divisor and the numerator is the dividend.

Conclusion:

Use this online difference quotient calculator with steps for finding the derivative of quotients, which is the difference quotient between two different points as they get closer to each other. This free difference quotient solver approximates numerical differentiation and finds f(x+h)-f(x)/h for the difference quotient quickly.

References:

From the source of Wikipedia: Difference quotient, Defining the point range, Applying the divided difference
From the source of Cuemath: Difference Quotient Formula, What Is the Difference Quotient Formula?, Difference Quotient Formula, Difference Quotient Formula Derivation