Euler's Method Calculator

An online Euler’s method calculator helps you to estimate the solution of the first-order differential equation using the eulers method. Euler’s formula Calculator uses the initial values to solve the differential equation and substitute them into a table. Let’s take a look at Euler’s law and the modified method.

What is Euler’s Method?

The Euler method (also known as the forward Euler method) is a first-order numerical method used to solve ordinary differential equations (ODE) with specific initial values. This is the most explicit method for the numerical integration of ordinary differential equations.

However, an Online E Calculator that allows you to calculate the value of e to the power of x. Here “X” can be any power or a number value of your choice and e is the exponent.

Euler’s Method Formula:

Many different methods can be used to approximate the solution of differential equations. So, understand the Euler formula, which is used by Euler’s method calculator, and this is one of the easiest and best ways to differentiate the equations. Curiously, this method and formula originally invented by Eulerian are called the Euler method.

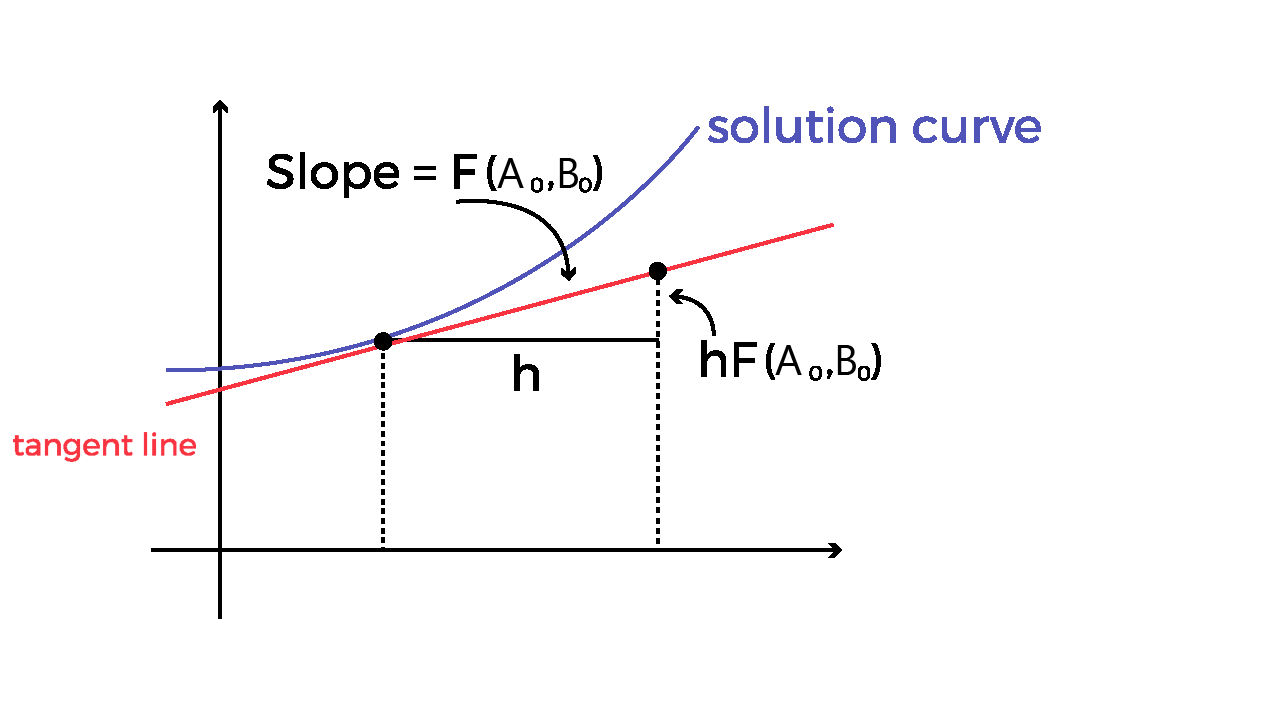
$$A_n = A_{n-1} + hA (B_{n-1}, A_{n-1})$$

Example:

Given the initial value problem

x’= x, x(0)=1,

For four steps the Euler method to approximate x(4).

Using step size which is equal to 1 (h = 1)

The Euler’s method equation is \(x_{n+1} = x_n +hf(t_n,x_n)\), so first compute the \(f(t_{0},x_{0})\).

Then, the function (f) is defined by f(t,x)=x:

$$f(t_{0},x_{0})=f(0,1)=1.$$

The slope of the line, which is tangent to the curve at the points (0,1). So, the slope is the change in x divided by the change in t or Δx/Δt.

multiply the above value with the step size h:

$$f(x_0) = 1 . 1 = 1$$

Since the step is the change in the t, when multiplying the slope of the tangent and the step size, we get a change in x value.

By substituting the initial x value in the euler method formula to find the next value. Also, you can find these values with euler’s method calculator.

$$x_0 + hf(x_0) = x_1 = 1 + 1 . 1 = 2$$

By repeating the above steps to find x_{2},x_{3} and x_{4}.

$$x_2 = x_1 + hf(x_1) = 2 + 1 . 2 = 4$$

$$x_3 = x_2 + hf(x_2) = 4 + 1 . 4 = 8$$

$$x_4 = x_3 + hf(x_3) = 8 + 1 . 8 = 16$$

Due to the repetitive nature of this eulers method, it can be helpful to organize all computation in an Euler’s method table.

Hence, the calculation is that x_{4}=16. The exact solution of this differential equation is: $$x(t)=e^{t}, so x(4)=e^{4} = 54.598$$

However, an Online Linear Approximation Calculator helps you to calculate the linear approximations of either parametric, polar, or explicit curves at any given point.

How Euler’s Method Calculator Works?

An online Euler method calculator solves ordinary differential equations and substitutes the obtained values in the table by following these simple instructions:

Input:

• Enter a function according to Euler’s rule.
• Now, substitute the value of step size or the number of steps.
• Then, add the value for y and initial conditions.
• “Calculate”

Output:

• The Euler’s method calculator provides the value of y and your input.
• It displays each step size calculation in a table and gives the step-by-step calculations using Euler’s method formula.
• You can do these calculations quickly and numerous times by clicking on recalculate button.

FAQ for Euler Method:

What is the step size of Euler’s method?

Usually, Euler’s method is the basis for creating more complex methods. Euler’s method is based on the fact that near a point, the meaning of the function and its tangent is almost the same. Change the x coordinate, also known as the step size.

Can you use the Euler method in the opposite direction?

In numerical analysis and scientific calculations, the inverse Euler method (or implicit Euler method) is one of the most important numerical methods for solving ordinary differential equations. It is similar to the (standard) Euler method, but the difference is that it is an implicit method.

Why is Euler more stable in the backward direction?

The forward and backward Euler schemes have the same accuracy limits. However, the inverse Euler method is implicit, so it is a very stable method for most problems. Therefore, when solving linear equations (such as Fourier equations), the inverse Euler method is stable.

What are the disadvantages of Euler’s method?

Euler’s method makes the pendulum simple. Advantages: Euler’s method is simple and straightforward. Can be used for non-linear IVP. Disadvantages: low accuracy and unstable value. The Euler’s approximation error is proportional to the step size h.

Why is Runge-Kutta more accurate?

High-order RK methods are multi-level because they include multi-level slope calculations between the current value and the next discrete time value.

Conclusion:

Use this online Euler’s method calculator to approximate the differential equations that display the size of each step and related values in a table using Euler’s law.  Of course, manually it is difficult to solve the differential equations by using Euler’s method, but it will become handy when the improved Euler method calculator is used.

Reference:

From the source of Wikipedia: Euler method, Informal geometrical description, MATLAB code example, R code example, Using other step sizes, Local truncation error, Global truncation error, Numerical stability, Rounding errors, Modifications and extensions.

From the source of Delta College: Summary of Euler’s Method, A Preliminary Example, Applying the Method, The General Initial Value Problem.

From the source of Brilliant: Euler’s Method, The Method, Effects of Step Size, Subsequent Steps.

From the source of Paul’s Notes: Intervals of Validity section, Uses of Euler’s Method, a bit of pseudo-code, Approximation methods.