Adblocker Detected
We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators.
Disable your Adblocker and refresh your web page 😊
How Was Your Calculator Experience? 
We'd Welcome your Feedback
Thank you for visiting our website. You have been selected to participate in a brief customer satisfaction survey to let us know how we can improve your experience
No, Thanks
Table of Content
The reciprocal calculator swiftly finds the reciprocal of different types of numbers, integers, simple fractions, and mixed fractions.
Through this tool, you can easily get the multiplicative inverse of any number or fraction along with the step-by-step calculation.
The procedure of finding the reciprocal of an integer/decimal, simple, and mixed fractions is as follows:
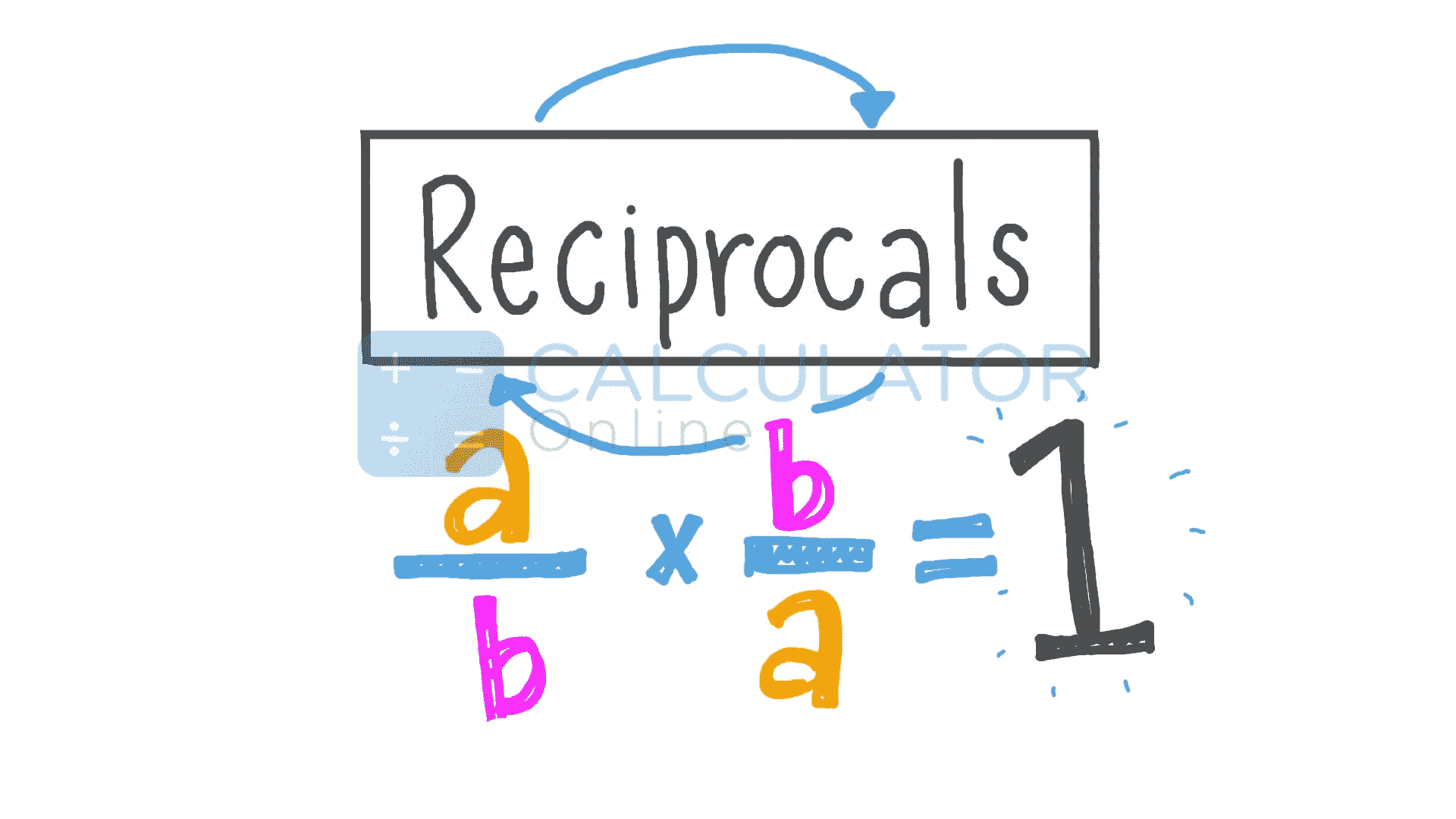
First of all, divide it by 1 to make a numerator:
After that perform swapping of numerator and denominator as below:
The reciprocal of 24.75 is:
\(\dfrac{24.75}{1} 🔀 \dfrac{1}{24.75}\)
\(\dfrac{1}{24.75}\ is\ a\ reciprocal\ of\dfrac{1}{24.75}\)
Change the decimal to fraction:
\(\dfrac{1\times100}{24.75\times 100}=\dfrac{100}{2475}=\dfrac{4}{99}\)
Swap the numerator and denominator:
\(\dfrac{20}{24} 🔀 \dfrac{24}{20}=\ 1.2\)
\(\dfrac{24}{20}=\ is\ a\ reciprocal\ of\ \dfrac{20}{24}\)
Solve the proper fraction and then flip it into its reciprocal as below:
\(\ 3\dfrac{4}{5}=\dfrac{19}{5} 🔀 \dfrac{5}{19}=\ 1.2\)
To precisely compute the reciprocals of the decimals/numbers, fractions, and mixed fractions, use the reciprocal calculator. It simplifies the process of finding the multiplicative inverse.
Lets suppose you have the following mixed fraction, find the reciprocal:
\(\ The\ mixed\ fraction=\ 3\dfrac{5}{7}\)
Solution:
Change the mixed fraction to a simple fraction by multiplying the “7” by “3” and adding “5”:
We get
\(\ Mixed\ fraction=\ 3\dfrac{5}{7}=\dfrac{21+5}{7}=\dfrac{26}{7}\)
Now we have the improper fraction. Converting the numerator to the denominator and vice versa:
\(\dfrac{26}{7},\ we\ get\ \dfrac{7}{26}\)
By multiplying:
\(\dfrac{26}{7}\times\dfrac{7}{26}=\ 1\)
You can perform the manual calculations as we have done above, or for convenience, you can use the reciprocal fraction calculator.
A negative reciprocal has a negative sign before the number. The negative reciprocal is specially designed for negative numbers and fractions.
\(\ Examples:\dfrac{-7}{1}.\dfrac{-4}{3}, \ -5\dfrac{3}{2}\ etc\)
A reciprocal of the unIty or “1” is one Itself. For this, find the inverse of “1” as:
\(\dfrac{1}{1}(i.e.\dfrac{1}{1} =\ 1)\ and \ (1\times 1 =\ 1)\)
The simple rule of the division is “Multiply the dividend by the reciprocal of the divisor”, simply you need to invert the divisor and multiply It by the dividend.
References:
From the source of Wikipedia: Multiplicative inverse, Examples and counterexamples
From the source of expii.com: Explanation, Turn that Frown Upside Down
Get the ease of calculating anything from the source of calculator online
Powered By:
Other Website:
Email us at
We are Located at
71-75 Shelton Street, Covent Garden London
Follow Us
© Copyrights 2024 by Calculator-online.net
