Summation Calculator

Find the sum of a number series with the summation calculator. The tool also supports the summation of algebraic expressions with lower and upper ranges entered.

With that, get step-wise solution also helps you to understand the calculations more deeply.

What Is Summation?

In Mathematics:

“Summation is the addition process of any numbers called the summands or addends that result in the sum or total”

The sequence is the series that defines the mathematical operation “+”.

Summation Symbol: Σ (A Greek Letter)

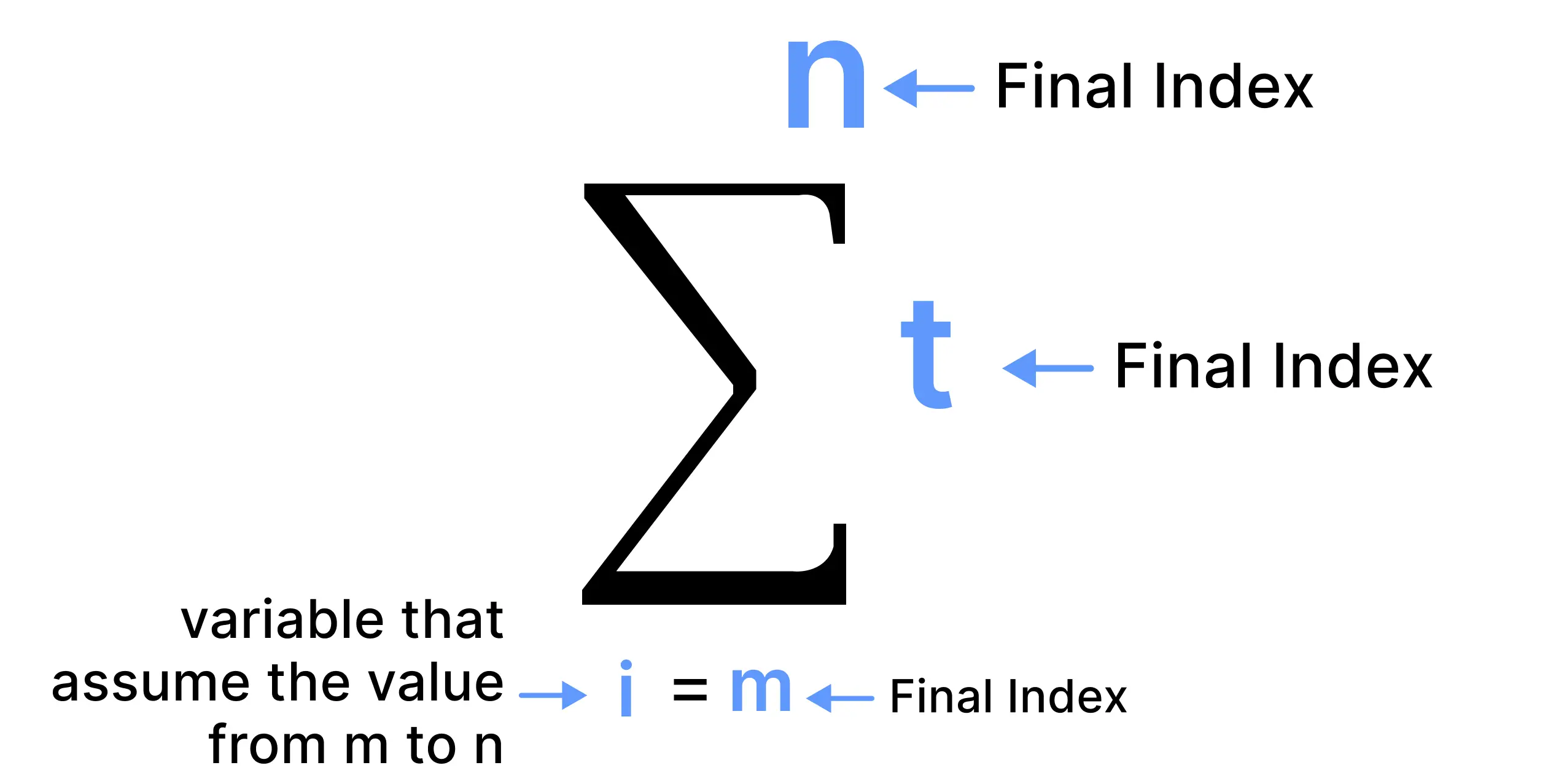
summation

Summation Formula:

The basic sigma equation is as follows:

\(\sum_{n=1}^n x_i = x_1 + x_2 + x_3 + … + x_n\)

Where:

i = Lower bound
n = Upper bound

How to Calculate a Summation?

Example # 01:

Suppose we have the first ten composite numbers listed as:

4, 6, 8, 9, 10, 12, 14, 15, 16, 18

Their sum is calculated as follows:

Step # 01: Write all numbers with an addition sign in between them

Sum = 4 + 6 + 8 + 9 + 10 + 12 + 14 + 15 + 16 + 18

Answer:

Sum = 112

Example # 02:

If you have a given expression in the sigma notation below:

\(\sum_{n=3}^7 x_{i}^3\)

You may evaluate summation by expanding the sigma notation, which can be done as follows:

Step # 01: Write down the lower and upper limits

Lower limit = 3
Upper limit = 7

Step # 02: Now write the original function in the summation notation

\(\sum_{n=3}^7 x_{i}^3 = x_{3}^3 + x_{4}^3 + x_{5}^3 + x_{6}^3 + x_{7}^3\)

Step # 03: Enter the actual values

\(\sum_{n=3}^7 x_{i}^3 = 3^3 + 4^3 + 5^3 + 6^3 + 7^3\)

Step # 04: Solve to the most simple sigma notation

\(\sum_{n=3}^7 x_{i}^3 = 3^3 + 4^3 + 5^3 + 6^3 + 7^3\)

\(\sum_{n=3}^7 x_{i}^3 = 27 + 64 + 125 + 216 + 343\)

\(\sum_{n=3}^7 x_{i}^3 = 775\)

Types of Summation:

Summation is of two types that include:

Simple Series Sum:

2+3+4+5+65+6+6=91

Description:

Simple summation represents a simple arithmetic sum of numbers.

Sigma Notation:

\(\sum_{i=0}^{n} [f\left(x\right)]\)

Description:

This formula is expanded to evaluate the final sum. We have to start from the Index (Lower Limit) and terminate at the Endpoint (Upper Limit).

Important Summation Equations:

Sigma (Summation) for	Formula
Sum of natural numbers	^mΣ_x=1 x = [m(m + 1)]/2
Sum of squares of natural numbers	^mΣ_x=1 x² = [m(m + 1)(2m + 1)]/6
Sum of cubes of natural numbers	^mΣ_x=1 x³ = [m²(m + 1)²]/4
Sum of 4^th power of natural numbers	^mΣ_x=1 x⁴ = [m(m + 1)(2m + 1)(3m² + 3m – 1)]/30
Sum of 1^st m even numbers	^mΣ_x=1 2x = m(m + 1)
Sum of 1^st m odd numbers	^mΣ_x=1 (2x + 1) = m²
Sum of an arithmetic sequence	^mΣ_x=1 a + (x – 1)d = m[2a + (m – 1)d]/2

How Do I Do Double Summation?

First, change the order of expression for double sums
Now, the external-sum index is holding and increases the internal index
After using the internal sum index, increase the external sum index
Repeat the previous steps for the entire external sum index