Transformer Calculator

The transformer calculator finds the primary and secondary full load currents (Amps) and voltages of single and 3-phase transformers. It can function to make calculations for both ideal and real transformers and identify their types based on the turns ratio. Moreover, the tool also helps you estimate EMF & different transmission losses including

Eddy Current Loss
Total Iron Loss
Total Copper Loss
Hysteresis Loss

What Is A Transformer?

A transformer operates to deliver current from one AC circuit to one or more AC circuits. This component works according to Faraday’s Law of Electromagnetic Induction to either step up or down the voltage.

Symbol:

Transformer Formulas:

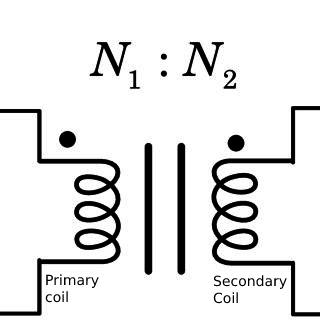
Transformer calculator considers the following equations that help you analyze a mathematical model of the transformer.

Voltage Equation:

\(V_p = N_p / N_s × V_s\)

Where:

\(V_p\) = Primary Coil Voltage
\(V_s\) = Secondary Coil Voltage
\(n_p\) = Number of Turns on Primary Coil
\(n_s\) = Number of Turns on Secondary Coil

Equivalent Current Equation:

\(I_s=I_p*\dfrac{N_p}{N_s}\)

Load Currents:

Single-Phase:

\(Full-Load Current (Amps)= kVA × 1000 / V\)

Three-Phase:

\(Full-Load Current (Amps) = kVA × 1000 / (1.732 × V)\)

Turns Ratio:

\(Turns Ratio = N_1 / N_2 = V_1 / V_2 = I_2 / I_1\)

Example:

Consider a single phase transformer of size about 56kVA. Its primary voltage is 350 volts and secondary voltage is almost 120 volts. Considering the transformer to be the ideal one, calculate the turns ratio and full load current range.

Solution:

As the transformer is supposed to be ideal one: Turns Ratio = N1 / N2 = V1 / V2 = (350 / 76) = 4.60 Determining the full load currents:

Primary:

\(Primary Full-Load Current (Amps)= kVA × 1000 / V\)

\(Primary Full-Load Current (Amps)= 56 × 1000 / 350\)

\(Primary Full-Load Current (Amps)= 56 × 2.857\)

\(Primary Full-Load Current (Amps)= 159.992\)

Secondary:

\(Secondary Full-Load Current (Amps)= kVA × 1000 / V\)

\(Secondary Full-Load Current (Amps)= 56 × 1000 / 120\)

\(Secondary Full-Load Current (Amps)= 56 × 8.333\)

\(Secondary Full-Load Current (Amps)= 466.648\)

Related: Do not forget to calculate Voltage Drops and Amperage across different circuits while analyzing the functionality of a transformer.

How To Size a Transformer?

To size a transformer effectively, you can use the given equation. All you need to simply multiply the amperes with the secondary output voltage.

Mathematically:(VA) = Secondary Voltage * Required Current

Important:

We do not recommend loading a transformer above 80% of its KVA rating. To find the minimum KVA rating needed, divide the calculated KVA by a factor of 0.8. All values should be reviewed and confirmed by an electrician or electrical engineer.

Transformer Amperage Chart:

Single Phase Transformers, Full Load Amperes (FLC):

KVA	120V	208V	240V	277V	480V	600V
.25	1.2	1.	0.9	0.5	0.4
.50	4.2	2.4	2.1	1.8	1.0	0.8
.75	6.3	3.6	3.1	2.7	1.6	1.3
1	8.3	4.8	4.2	3.6	2.1	1.7
1.5	12.5	7.2	6.2	5.4	3.1	2.5
2	16.7	9.6	8.3	7.2	4.2	3.3
3	25	14.4	12.5	10.8	6.2	5
5	41	24	20.8	18	10.4	8.3
7.5	62	36	31	27	15.6	12.5
10	83	48	41	36	20.8	16.7
15	125	72	62	54	31	25
25	206	120	104	90	52	41
37.5	312	180	156	135	76	62
50	416	240	208	180	104	83
75	625	340	312	270	156	125
100	833	480	416	361	208	166
167	1391	803	695	603	347	278

Three Phase Transformers, Full Load Amperes (FLC):

KVA	208V	240V	480V	600V
3	8.3	7.2	3.6	2.9
6	16.6	14.4	7.2	5.8
9	25	21.6	10.8	8.6
15	41.7	36.1	18.0	14.4
30	83.4	72.3	36.1	28.9
45	124	108	54.2	43.4
75	208	180	90	72
112.5	312	270	135	108
150	416	360	180	144
225	624	541	270	216
300	832	721	360	288
500	1387	1202	601	481
750	2084	1806	903	723
1000	2779	2408	1204	963

Insulation Class and Temperature Rise:

KVA		Insulation
1 Phase	3 Phase	NEMA Class	Temperature Class	Temperature Rise
0.25-25	3-15	F	180° C	115° C
15-167	15-1000	H	220° C	150° C