Trapezoidal Rule Calculator

An online trapezoidal rule calculator helps you to estimate the area under the graph of the given function using the trapezoidal rule.  The free trapezoid area calculator approximates the integral in multiple subintervals with step-wise calculations. Have a look at the trapezoidal rule and sum formula in the below context.

What is the Trapezoidal Rule?

In numerical analysis, the trapezoidal rule is a method for estimating the definite integral.

∫^x_y f(y) dy

The trapezoid rule works by estimating the area under the graph of a function f(y) as a trapezium and computing its area with:

∫^x_y f(j) dj = ( x – y) . f(x) + f(y) / 2

The trapezoidal rule calculator used the Trapezium method to estimate the definite integrals.

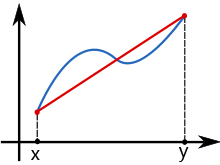
However, the Online Integral Calculator allows you to find the integrals of the functions with respect to the variable involved.

Area of Trapezoidal

(Image)

Now, the area of a trapezium is given by:

Area = h/2 (a + b)

Where,

h = height of rectangular

How to Solve Integral Function Using Trapezoidal Rule?

Follow these guidelines to calculate any function area using trapezoidal rule manually.

• First, pick a function with integration and lower, upper limits.
• Now, trapezoidal sum formula to determine the trapezoid rule of the function is

$$∫^x_y f(a)da ≈ Δa/2 [f(a^0) + 2f(a^1) +. . . +2f(a^{n-1}) + f(x^n), \text { where} , Δa = (y-x)/n.$$

• Divide the interval into smaller trapezoids of length Δa.
• In the subintervals last one is y and the first one is x, and evaluate the functions at those trapezoids values.
• Plug the values in the trapezoidal rule formula and sum up the obtained values to get the estimated value.

However, an Online Riemann Sum Calculator will help you to approximate the definite integral and sample points of midpoints, trapezoids, right and left endpoints using finite sum.

Example:

Use the Trapezoidal Rule with n = 5 to estimate:

$$∫^{x=0}_{y=1} \sqrt{(1+sin3(y)}$$

Solution:

The function f is:

$$f(a) = \sqrt{(1+sin3(a)}$$

$$x= 0, y= 1, n=5.$$

According to Trapezoidal Rule:

$$∫^y_x f(a)da ≈ Δa/2 [f(a^0) + 2f(a^1) +. . . +2f(a^{n-1}) + f(a^n)$$

$$Δa = (y-x)/n$$

Substitute the given values in the above formula to get Δa value.

$$Δa = 1-0/5 = 1/5$$

Divide the interval [0,1] into n=5 subintervals of length Δa=1/5, with the following endpoints:

$$x = 0, 1/5, 2/5, 3/5, 4/5, 1= y$$

Evaluate the function with trapezoidal rule calculator at these end points:

$$f(a^0) = f(x) = f(0) = √(1+sin3(0) = 1$$

$$2f(a^1) = 2f(1/5) = 2√(1+sin3(1/5) = 2.0078$$

$$2f(a^2) = 2f(2/5) = 2√(1+sin3(2/5) = 2.0582$$

$$2f(a^3) = 2f(3/5) = 2√(1+sin3(3/5) = 2.1725$$

$$2f(a^4) = 2f(4/5) = 2√(1+sin3(4/5) = 2.3402$$

$$f(a^5) = f(1) = 2√(1+sin3(1) = 1.2632$$

$$Δa/2 = 1/10$$

Finally sum up the above values and multiply by Δa/2

$$= 1/10 (1 + 2.0078 + 2.0582 + 2.1725 + 2.3402 + 1.2632)$$

$$= 1.0842$$

How Trapezoidal Rule Calculator Works?

An online trapezoidal approximation calculator will provide the approximate region using the trapezoid method by these steps:

Input:

• First, enter a function with respect to different variables.
• Now, substitute the upper and lower limit.
• Then, add the number of trapezoids as per requirement.
• Click on the “Calculate” button to see the results.

Output:

• The trapezoidal rule calculator displays your input and answer in standard form.
• The area of a trapezoid calculator provides all endpoints and the sum of these points.

FAQ:

Is the trapezium rule the same as Simpson's rule?

Simpson's Rule can be referred to as Parabolic Rule. But, the trapezoidal rule can be referred to as the Trapezoid rule.

Which rule is better trapezoidal or Simpsons?

When we work with quadratic functions, the Simpsons rule provides the best estimation and the Trapezoidal provided the worst approximation. As well, for the trigonometric functions, the Simpsons method also gave the most accurate estimation while the Trapezoid gave the least accurate estimation.

Conclusion:

Use this free online trapezoidal rule calculator which is made for researchers, students, mathematicians, and teachers. This handy area of the trapezoid calculator takes the integral function with upper and lower limits and quickly provides a 100% accurate step-by-step solution.

Reference:

From the source of Wikipedia: Trapezoidal rule, Numerical implementation, Non-uniform grid, Uniform grid.

From the source of Math 24: Riemann Sums, little trapezoids, definite integral, Trapezoidal Rule.

From the source of LibreText: Numerical Integration - Midpoint, Trapezoid, Simpson's rule, The Midpoint Rule.