Diagonal Calculator

The diagonal calculator measures the diagonal, area, perimeter, and diagonal angle of a rectangle.  You just need to enter only two values to find the diagonal of the rectangle.

Diagonal of a Rectangle: 

A Rectangle is a quadrilateral having four angles and all the angles are 90 degrees. The opposite sides of the rectangle are parallel and equal in length. The adjacent sides of the rectangle are different in length, but the diagonals are equal in length and intersect in the middle point of the rectangle. We need to enter the length and width in the rectangle diagonal calculator to find the diagonal of the rectangle.

How to Find the Diagonal of a Rectangle?

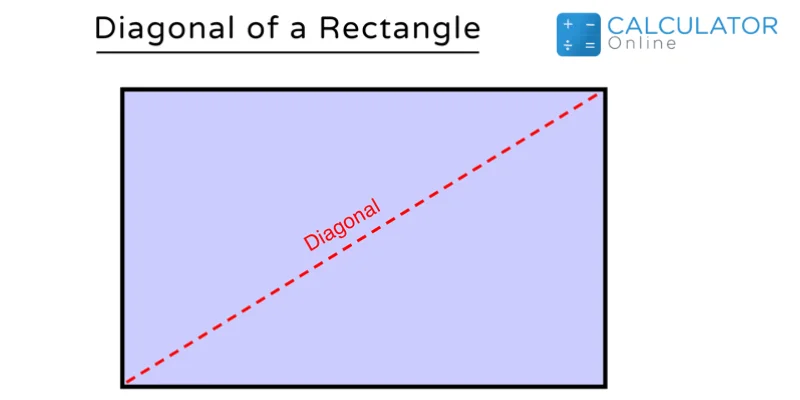
We can find diagonal of a rectangle as:

Diagonal = √(l² + w²) 

Where:

I = Length of the Rectangle

W = Width of Rectangle

Area of a Rectangle:

We can find the Area of the Rectangle by multiplying the length and width:

Area = l× w

The Perimeter of a Rectangle:

The perimeter of the rectangle can be measured by the given formula:

Perimeter = 2l + 2w=2(l+w)

Possibilities of Diagonal of Rectangle Measurements:

We can encounter various possibilities to find diagonal of a rectangle.

From Area and Length:

First, we have to find the length by the given formula:

l= A /w 

Then,

P = 2l + 2w

Diagonal length of a rectangle = √(l² + w²) 

From  Area and Width:

First, we have to find the width:

w= A / l

P = 2l + 2w

The diagonal measurement of a rectangle can be done as:

Diagonal = √(l² + w²) 

From  Perimeter and Length:

w = (P – 2l) / 2

Area = l× w

Diagonal = √(l² + w²) 

From  Perimeter and Width:

l= (P – 2w) / 2

Area = l× w

Diagonal = √(l² + w²) 

Practical Example:

Measure the length of the diagonal, area, and perimeter of a rectangle whose length is 4 units and width is 3 units.

Sol:

Length   = 4 units

Width   = 3 units

Substituting the values in the below equation

 Diagonal = √(l² + w²)= √(4² + 3²)  = √(25²).

The rectangle diameter = 5 units.

 Length of diagonal of a rectangle= 5 units.    

Area of rectangle = l× w

Area of rectangle = 4× 3 = 12 unit²

Perimeter of the rectangle  = 2l + 2w 

Perimeter of the rectangle  = 2(4) + 2(3)

The perimeter of the rectangle  = 8+ 6

The perimeter of the rectangle  = 14 units

How to Use a Diagonal Calculator?

Stick  to the following steps for precise calculations by the diagonal measurement calculator

Input:

Enter any two of the given input and Hit the calculate button 

Output:

• The diagonal of a rectangle
• The Area of a rectangle
• The Perimeter of a rectangle
• The circumcircle of a rectangle
• The angle of a rectangle

References:

From the source of wikipedia.org: Circumscribed circles>,Triangles

From the source of wikihow.com: Diagonal,Length, and the Width