Combination Calculator

An online number combination calculator allows you to find the number of possible combinations that can be obtained from the sample items from the large dataset. Also, this combinatorics calculator shows you the every single combination of the dataset. Basically, combination is the number of ways to get the r elements from the n objects of dataset where replacements are not allowed.

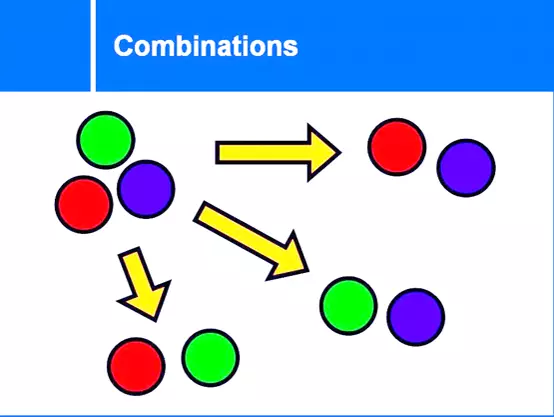
Give a complete read of the article to exactly know about its formula, manual calculation, how to find combination with this combinations calculator and much more. Also, you can try our online permutation calculator that helps you to find the number of possible subsets including the subset of same item in different order. Read on!

What is the Combination Formula?

The formula to determine the number of possible combinations is as follows:

$$  C(n,r) = \frac{n!}{r!(n-r)!} $$

Where,

n is the total number in the dataset

r is the number you select from this dataset & _nC_r is the number of combinations

Our ncr calculator uses this formula for the accurate & speedy calculations of all the elements of the dataset.

Formula for Combination with Repetition:

If we don’t care about the repetition, then the ncr formula is:

$$ C(n,r)  = \frac{(r+n-1)!} { r! (n-1)!} $$

The exclamation mark (!) used for the factorial of the number. To find the factorial of the number, you can also try our online factorial calculator that helps you to calculate the factorial of the given n numbers.

How to Calculate Combinations (Step-by-Step):

Here we have different combinations examples that will help you to find out the different combinations of your desired numbers. Also, this combinatorial calculator gives you each & every combination of your given input accurately. Ahead to some manual examples: Swipe on!

Example 1:

The Principal select 4 students from the class with 30 total students to compete in the athletics. He want to determine how many Combinations of 4 students can be generated from 30 students?

Solution:

The combination equation is:

$$ C(n,r) = \frac{n!}{ r! (n-r)!} $$

Here,

The total numbers of students

(n) = 30 Chosen students

(r) = 4

So,

$$ C(30,4) = \frac{30!}{ 4! (30-4)!} $$

$$ C(30,4) = \frac{30!}{4! (26)!} $$

$$ C(30,4) = \frac{30*29*28*27*26! }{4! (26)!} $$

$$ C(30,4) = \frac{30*29*28*27}{ 4!} $$

$$ C(30,4)  = \frac{30*29*28*27}{4*3*2*1} $$

$$ C(30,4) = \frac{657720}{24} $$

$$ C(30,4) = 27405 Possible teams $$

Here we have another example for further understanding:

Example 2:

A restaurant wants to pick their 6 favorite deserts from the total 24 deserts. How many different combinations the customer picks?

Solution:

The combination equation is:

$$ C(n,r) = \frac{n!}{ r! (n-r)!} $$

Here,

The total numbers of deserts (n) = 24

Chosen deserts (r) = 6

So,

$$ C(24,6) = \frac{24!}{ 6! (24-6)!} $$

$$ C(24,6) = \frac{24!}{6! (18)!} $$

$$ C(24,6) = \frac{24*23*22*21*20*19*18! }{6! (18)!} $$

$$ C(24,6) = \frac{24*23*22*21*20*19}{6!} $$

$$ C(30,4)  = \frac{24*23*22*21*20*19}{6*5*4*3*2*1} $$

$$ C(30,4) = \frac{96909120}{720} $$

$$ C(30,4) = 134596 $$

You can also verify the results with the assistance of this best combination calculator.

Example 3:

If I have 3 tin cans, then how many ways can i give these three tin cans to 8 people?

Solution:

The combination equation is:

$$ C(n,r) = \frac{n!}{ r! (n-r)!} $$

Here,

The total numbers of people(n) = 8

Chosen people(r) = 3

So,

$$ C(8,3) = \frac{8!}{3! (8-3)!} $$

$$ C(8,3) = \frac{8!}{3! (5)!} $$

$$ C(8,3) = \frac{8*7*6*5! }{3! (5)!} $$

$$ C(8,3) = \frac{8*7*6}{3!} $$

$$ C(8,3)  = \frac{8*7*6}{3*2*1} $$

$$ C(8,3) = \frac{336}{6} $$

$$ C(8,3) = 56 $$

You can try this online combinations calculator to verify all the combinations example for the clarification.

Combinations & Permutations:

In English language, we use the word combination without thinking the order is important or not. Simply, my lunch consists of Burger, Reuben sandwich and Apple pie. We don’t care about their order they could also be in “Reuben sandwich, Apple pie and Burger”, but it’s the same food. Also,

The lock of the safe is 584. Now, if we don’t care about the order, then it doesn’t work. For example, 845 won’t work, not the 458 will work. We have to exactly enter 5-8-4. So, we concluded that:

When the order doesn’t matter, it is a combination while when the order matters, it is a permutation. In simple words, the permutation is the ordered combination.

How to Use the Online Combination Calculator:

The online number combination calculator requires different values for accurate calculation, these are the steps you ought to follow to get the instant results.

Inputs:

• First of all, choose the name of the elements of dataset from the dropdown of this tool.
• Very next, enter the total number of elements in the designated field.
• Then, enter how many elements you want to choose from the total elements.
• Next you have to select which you want to generate from dropdown menu. It can either be combination or combination with repetition.
• Then, plug-in the values of elements in the designated field.
• Lastly, hit the calculate button.

Outputs: Once you done, the combination formula calculator shows:

• Combination
• Combination with repetition
• Step-by-step calculation

Note: Quit worrying either you want to get the calculation with combination or repetition, all you need to choose the respective option, the combinations calculator will shows you the result according to the given values.

Frequently Ask Questions (FAQ’s):

What do 10 choose 3 mean?

It means choosing the 3 elements from the 10 total elements without any order or repetition. It generates the result of 120 possible combinations.

What is combination used for?

It determines the possible arrangements in the collection of n items. It helps to select the items in any order. This condition is not clear with the permutation of the number.

End-Note:

Thankfully, you come to know that combinations are used to determine the possible arrangements in the collection n items. When it comes to the calculation of the large number, use free online combination calculator that helps you to find the combination of the given elements.

nCr Quick Reference Table:

The given table helps you to check what are all the combinations for n distinct objects taken r at a time:

References:

From the authorized source of Wikipedia : Definition & formulas with complete manual calculation From the site of britannica : Difference between Combination & Permutation From the source of math.stackexchange : How to find all possible combinations of a set of options.